Il Teorema di Bayes Un Approccio Probabilistico

Introduzione al concetto di Bayes

Il teorema di Bayes è un principio fondamentale della probabilità che fornisce un metodo per aggiornare le nostre credenze sulla base di nuove informazioni. È un concetto potente che trova applicazione in una vasta gamma di campi, dalla medicina all’intelligenza artificiale.

Definizione e importanza del teorema di Bayes

Il teorema di Bayes è una formula matematica che descrive la probabilità di un evento, dato che un altro evento è già avvenuto. In termini più semplici, ci dice come aggiornare la nostra conoscenza di un evento in base a nuove prove.

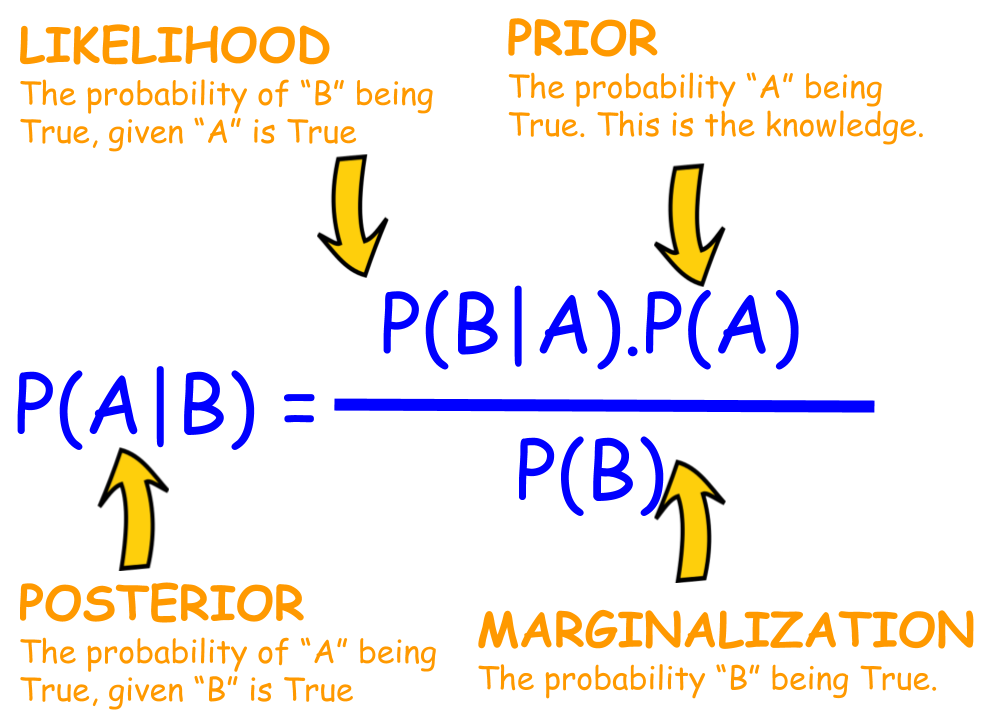
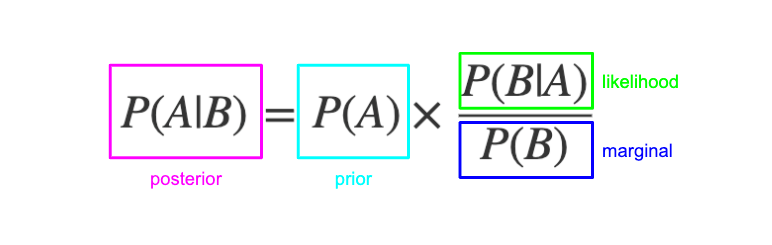
P(A|B) = [P(B|A) * P(A)] / P(B)

Dove:

* P(A|B) è la probabilità di A dato che B è avvenuto (probabilità a posteriori).
* P(B|A) è la probabilità di B dato che A è avvenuto (probabilità verosimiglianza).
* P(A) è la probabilità di A (probabilità a priori).
* P(B) è la probabilità di B.

L’importanza del teorema di Bayes risiede nella sua capacità di aggiornare le nostre credenze in modo sistematico e razionale. Ci permette di incorporare nuove informazioni per migliorare le nostre previsioni e decisioni.

Basi matematiche del teorema di Bayes

Il teorema di Bayes si basa sul concetto di probabilità condizionata. La probabilità condizionata è la probabilità di un evento, dato che un altro evento è già avvenuto. In altre parole, è la probabilità di un evento A, sapendo che l’evento B è già accaduto.

La formula del teorema di Bayes deriva dalla definizione di probabilità condizionata:

P(A|B) = P(A e B) / P(B)

Possiamo anche scrivere:

P(B|A) = P(A e B) / P(A)

Combinando queste due equazioni, otteniamo il teorema di Bayes:

P(A|B) = [P(B|A) * P(A)] / P(B)

Esempio pratico

Immaginiamo di avere un test medico per una malattia rara. Il test ha un’accuratezza del 95%, il che significa che il 95% delle persone malate risulta positivo al test, mentre il 5% risulta negativo. Inoltre, sappiamo che la malattia colpisce lo 0,1% della popolazione.

Ora, supponiamo che una persona risulti positiva al test. Qual è la probabilità che la persona sia effettivamente malata?

Possiamo usare il teorema di Bayes per rispondere a questa domanda.

* A = la persona è malata
* B = il test risulta positivo

* P(A) = 0,001 (probabilità a priori di essere malati)
* P(B|A) = 0,95 (probabilità di un test positivo dato che si è malati)
* P(B|non A) = 0,05 (probabilità di un test positivo dato che non si è malati)
* P(B) = P(B|A) * P(A) + P(B|non A) * P(non A) = 0,95 * 0,001 + 0,05 * 0,999 = 0,0509 (probabilità di un test positivo)

Usando il teorema di Bayes, possiamo calcolare la probabilità che la persona sia malata, dato che il test è risultato positivo:

P(A|B) = [P(B|A) * P(A)] / P(B) = (0,95 * 0,001) / 0,0509 = 0,0187

Pertanto, la probabilità che la persona sia effettivamente malata, dato che il test è risultato positivo, è solo del 1,87%.

Differenze tra probabilità a priori e probabilità a posteriori

Nel contesto del teorema di Bayes, le probabilità a priori e a posteriori rappresentano due aspetti cruciali dell’inferenza probabilistica.

La probabilità a priori è la probabilità di un evento prima di osservare nuove informazioni. È la nostra credenza iniziale sull’evento, basata su informazioni precedenti o su ipotesi generali.

La probabilità a posteriori è la probabilità di un evento dopo aver osservato nuove informazioni. È la nostra credenza aggiornata sull’evento, tenendo conto delle nuove prove.

Nel nostro esempio del test medico, la probabilità a priori di essere malati è dello 0,1%. Questa è la nostra credenza iniziale sulla malattia, basata sulla sua prevalenza nella popolazione. Dopo aver osservato il risultato positivo del test, la nostra credenza si aggiorna alla probabilità a posteriori del 1,87%.

Il teorema di Bayes ci permette di passare dalla probabilità a priori alla probabilità a posteriori, incorporando le nuove informazioni e aggiornando le nostre credenze in modo sistematico.

Applicazioni del teorema di Bayes

Il teorema di Bayes, con la sua capacità di aggiornare le probabilità alla luce di nuove informazioni, ha trovato applicazioni in un’ampia gamma di settori, influenzando significativamente il modo in cui analizziamo i dati e prendiamo decisioni.

Applicazioni in medicina

Il teorema di Bayes è ampiamente utilizzato in medicina per la diagnosi delle malattie. I medici possono usare questo teorema per calcolare la probabilità che un paziente abbia una particolare malattia, date le sue caratteristiche e i risultati dei test. Ad esempio, un medico può usare il teorema di Bayes per calcolare la probabilità che un paziente abbia il cancro al seno, dato che ha un risultato positivo a un mammogramma.

Il teorema di Bayes può essere applicato per calcolare la probabilità di avere una malattia (D) dato un risultato positivo a un test (T):

P(D|T) = [P(T|D) * P(D)] / P(T)

Dove:

P(D|T) è la probabilità di avere la malattia dato un risultato positivo al test.

P(T|D) è la probabilità di un risultato positivo al test dato che si ha la malattia (sensibilità del test).

P(D) è la probabilità di avere la malattia (prevalenza della malattia nella popolazione).

P(T) è la probabilità di un risultato positivo al test (probabilità di un risultato positivo sia in presenza che in assenza della malattia).

La sensibilità e la specificità del test sono fattori cruciali nel calcolo della probabilità di avere una malattia. La sensibilità si riferisce alla probabilità che il test risulti positivo se il paziente ha la malattia, mentre la specificità si riferisce alla probabilità che il test risulti negativo se il paziente non ha la malattia.

Applicazioni nell’intelligenza artificiale, Bayesian

Il teorema di Bayes è fondamentale per molti algoritmi di intelligenza artificiale, in particolare per i sistemi di classificazione e di apprendimento automatico. Questi sistemi usano il teorema di Bayes per classificare nuovi dati in base a informazioni precedenti. Ad esempio, in un sistema di riconoscimento facciale, il teorema di Bayes può essere utilizzato per classificare un’immagine come quella di una persona specifica, basandosi su caratteristiche come la forma del viso, gli occhi e il naso.

Applicazioni nella finanza

Il teorema di Bayes viene utilizzato nella finanza per la valutazione del rischio e la previsione dei prezzi delle azioni. Gli analisti finanziari possono usare questo teorema per aggiornare le loro previsioni sui prezzi delle azioni, basandosi su nuove informazioni come i risultati aziendali o i cambiamenti macroeconomici. Ad esempio, un analista finanziario può usare il teorema di Bayes per aggiornare la sua previsione sul prezzo di un’azione, dato che l’azienda ha annunciato un aumento dei profitti.

Applicazioni nella statistica

Il teorema di Bayes è un concetto fondamentale nella statistica inferenziale, che si occupa di trarre conclusioni da dati campionari. Il teorema di Bayes viene utilizzato per aggiornare le probabilità di ipotesi statistiche, basandosi su nuovi dati. Ad esempio, uno statistico può usare il teorema di Bayes per aggiornare la sua ipotesi sulla media di una popolazione, basandosi su un campione di dati.

Tabella delle applicazioni del teorema di Bayes

Tipo di problema	Applicazione
Diagnosi medica	Calcolo della probabilità di avere una malattia dato un risultato positivo a un test.
Riconoscimento facciale	Classificazione di un’immagine come quella di una persona specifica, basandosi su caratteristiche come la forma del viso, gli occhi e il naso.
Valutazione del rischio finanziario	Aggiornamento delle previsioni sui prezzi delle azioni, basandosi su nuove informazioni come i risultati aziendali o i cambiamenti macroeconomici.
Inferenza statistica	Aggiornamento delle probabilità di ipotesi statistiche, basandosi su nuovi dati.

Modelli bayesiani

I modelli bayesiani sono un approccio all’inferenza statistica che utilizza il teorema di Bayes per aggiornare le nostre credenze sulla base di nuove evidenze. Questo approccio differisce dai modelli frequentisti, che si basano sulla probabilità di un evento come la frequenza relativa con cui si verifica in un numero infinito di prove. I modelli bayesiani, invece, considerano la probabilità di un evento come una misura della nostra fiducia in un’ipotesi, basata sulle nostre conoscenze pregresse e sulle nuove informazioni disponibili.

Tipi di modelli bayesiani

Esistono diversi tipi di modelli bayesiani, ciascuno con le sue caratteristiche e applicazioni specifiche. Ecco alcuni esempi:

• Modelli lineari bayesiani: questi modelli estendono i modelli lineari tradizionali includendo una distribuzione di probabilità per i parametri del modello. Questo permette di considerare l’incertezza associata ai parametri e di ottenere inferenze più robuste.
• Reti bayesiane: queste reti grafiche rappresentano le relazioni di dipendenza tra diverse variabili. Ogni nodo della rete rappresenta una variabile e gli archi rappresentano le dipendenze tra le variabili. Le reti bayesiane possono essere utilizzate per modellare sistemi complessi e per effettuare inferenze probabilistiche sulle variabili di interesse.
• Modelli gerarchici bayesiani: questi modelli consentono di modellare la variabilità tra diversi gruppi di dati. Ad esempio, possono essere utilizzati per analizzare i dati provenienti da diverse scuole, considerando la variabilità tra le scuole e all’interno di ciascuna scuola. I modelli gerarchici bayesiani sono particolarmente utili quando si hanno dati limitati per ogni gruppo.

Vantaggi e svantaggi dei modelli bayesiani

I modelli bayesiani offrono diversi vantaggi rispetto ai modelli frequentisti, ma presentano anche alcuni svantaggi. Ecco un confronto tra i due approcci:

	Modelli bayesiani	Modelli frequentisti
Vantaggi	Permettono di incorporare le conoscenze pregresse nell’analisi. Forniscono una misura dell’incertezza associata alle stime dei parametri. Sono flessibili e possono essere utilizzati per modellare sistemi complessi.	Sono relativamente semplici da implementare. Sono ampiamente utilizzati e ben compresi.
Svantaggi	Possono essere computazionalmente costosi. La scelta della distribuzione a priori può influenzare i risultati.	Non permettono di incorporare le conoscenze pregresse. Possono essere sensibili alla dimensione del campione.

Bayesian methods, which utilize prior knowledge to update beliefs based on new evidence, find applications in diverse fields. Angela Bacares, a prominent figure in the field of data science , has championed the use of Bayesian techniques in her research, demonstrating their effectiveness in analyzing complex datasets and making informed decisions.

Bayesian inference, a statistical method that updates beliefs based on new evidence, can be applied to various fields, including the study of political systems. For example, analyzing the historical evolution of the repubblica in Italy, with its diverse political landscape, can provide valuable insights into the dynamics of democratic governance.

These insights can then be incorporated into Bayesian models to predict future political trends and inform policy decisions.